Ein Gastbeitrag von Prof. Dr. Thomas Rießinger und Michael Horn
„Gewöhnlich glaubt der Mensch, wenn er nur Worte hört“, lässt Goethe seinen Mephistopheles in der Hexenküche sagen, „es müsste sich dabei doch auch was denken lassen.“ Da wird man ihm gerne zustimmen, sich jedoch gleichzeitig an die eine oder andere Äußerung der Kanzlerin erinnern, deren pointierte und präzise Formulierungskunst den Zuhörer nicht nur zu der Frage veranlasst, was er sich nun im Sinne Mephistopheles’ dabei denken sollte, sondern auch zu dem weiterführenden Problem, ob sie sich selbst wohl irgendetwas dabei gedacht hat.
Aber nicht nur ganze Sätze – sofern man im Zusammenhang mit den erwähnten Äußerungen von so etwas sprechen kann –, sondern auch einzelne Worte, Schlagworte verschiedenster Art können sich zum Anwendungsfall für die zitierte Bemerkung entwickeln. In unserer Zeit, die uns allem Anschein nach mit der schlimmsten Pandemie aller Zeiten, gepaart mit einer an Fürsorglichkeit und Kompetenz kaum noch zu überbietenden Regierung heimgesucht hat, lautet das zentrale Wort „Inzidenz“, manchmal auch „Inzidenzwert“, und so mancher wird sich gefragt haben, ob „sich dabei doch auch was denken“ lässt und welche Gedankenwege möglich sind. Werfen wir also einen Blick auf das geheimnisvolle Wort.
Zunächst ist die Inzidenz nur eine Zahl wie andere auch, die auf eine bestimmte Weise berechnet wird – davon wird noch die Rede sein. Es sticht aber ins Auge, dass man Inzidenzen nach ihrer Größe beurteilen kann und vor allem, dass die Urteile schneller wechseln können als Karl Lauterbachs Talkshowsessel. Lag vor einiger Zeit das Heil noch bei einer Inzidenz von 50, so hat man vor Kurzem die 35 in den Rang des wünschenswerten Ziels erhoben – ergänzt noch um Tendenzen hin zum Wert 10 oder gar zur 0, – nur um dann vor wenigen Tagen dem erstaunten Publikum zu eröffnen, auch ein Wert von 100 sei schon recht brauchbar. Eine seltsame Kennzahl, so wichtig, wie man hört, und doch so beliebig, je nach Laune und Prioritäten der beteiligten Politiker.
Was ist nun mit diesem Rätselwort gemeint? Bei der AOK findet man die Information, die Inzidenz sei „eine Messgröße aus der Epidemiologie, die die Anzahl der Neuerkrankungen an einer bestimmten Krankheit in einer definierten Bevölkerungsgruppe während eines bestimmten Zeitraums angibt.“ Bei der 7-Tage-COVID-19-Inzidenz muss es sich folglich um die Anzahl der an COVID-19 Neuerkrankten innerhalb eines Zeitraums von sieben Tagen handeln. Im Glossar des RKI werden als Inzidenzfälle die Ereignisse gezählt, bei denen Personen innerhalb eines bestimmten Zeitraums vom Zustand „gesund“ in den Zustand „krank“ oder „betroffen“ wechseln, wobei man die Inzidenzrate erhält, indem man die Anzahl der Inzidenzfälle durch die mittlere Anzahl der jeweiligen Bevölkerung dividiert. Gezählt werden dabei auch und insbesondere Fälle, bei denen nichts weiter als ein positiver PCR-Test vorliegt.
Verwechslungsgefahr durch Virentrümmer
Hat man damit die Anzahl der Neuerkrankungen innerhalb der letzten sieben Tage festgestellt? Eher nicht. Zu nennen wäre hier zunächst das Problem des Ct-Wertes, also der Anzahl von Replikationszyklen, die man im Labor benötigte, um einigermaßen verwertbares genetisches Material zu erzeugen. Je höher die tatsächliche Virenlast, desto niedriger die notwendige Anzahl der Zyklen, und das heißt umgekehrt: Je höher die Anzahl der notwendigen Zyklen, desto geringer ist die reale Virenlast; man geht derzeit davon aus, dass die Grenze bei etwa 30 Zyklen liegt. Bei einem Ct-Wert von 30 oder darüber dürfte also nur in seltensten Fällen eine Erkrankung oder echte Infektiosität vorliegen. Da nun aber der Ct-Wert in der Meldepraxis keine Rolle spielt, ja oft genug nicht einmal verfügbar sein wird, werden in unbekannter Zahl irrelevante Fälle mit echten Fällen vermengt. Verschärft wird dieses Problem noch durch die Suchstrategie des PCR-Tests. Suchte man ursprünglich noch nach drei relevanten Genabschnitten, um sicherzustellen, dass man es nicht nur mit wirkungslosen Virentrümmern zu tun hat, schränkte man die Suche später auf zwei Abschnitte ein, um sich dann zu überlegen, dass ein einziges Ziel-Gen schon ausreichend sei. Das Risiko, bei einer derart eingeschränkten Suche Virentrümmer mit vollständigen und replikationsfähigen Viren zu verwechseln, ist nicht von der Hand zu weisen.
Zudem müssen die gefundenen positiven Fälle keineswegs neu sein. Hat man einmal Kontakt mit den entsprechenden Viren gehabt, werden zumindest ihre Restbestände noch deutlich länger als nur sieben Tage nachweisbar sein, insbesondere dann, wenn man mit den gerade beschriebenen Methoden vorgeht.
Kurz gesagt: Die gemeldeten Neuinfizierten sind unter Umständen weder neuinfiziert, noch neuinfiziert, man kann aufgrund der Messmethoden nicht feststellen, ob sie eine relevante Virenlast tragen bzw. ob ihre irgendwann vielleicht einmal vorhandene relevante Virenlast nur noch eine Erinnerung an frühere Zeiten ist. Man könnte zu der Auffassung kommen, dass schon dieser Umstand die Aussagekraft der Inzidenz doch etwas schmälert.
Berechnet wird die Inzidenz nach einer einfachen Formel: Man nimmt die Anzahl der innerhalb der letzten sieben Tage gemeldeten Fälle und bestimmt daraus die Anzahl der Fälle pro 100.000 Einwohner nach der Formel Fallzahl / Einwohnerzahl * 100000. Die Einwohnerzahl ist dabei die Anzahl der am 31.12.2019 vorhandenen Einwohner, für Deutschland also 83.166.711. An einem einfachen Beispiel, vor allem für Politiker und Journalisten des öffentlich-rechtlichen Rundfunks, kann man sich die Vorgehensweise klarmachen: Laut Lagebericht des RKI vom 8. März 2021 lagen in den letzten sieben Tagen 56.518 Fälle vor. Die Formel verlangt dann die Rechnung 56518 / 83166711 * 100000 = 67,96, was zu der im Bericht angegebenen Inzidenz von 68 führt. Somit hat es in den letzten sieben Tagen 68 Fälle pro 100.000 Einwohner gegeben.
Dunkelziffer unbekannt
Ist das so? Man darf daran zweifeln, und zwar nicht nur wegen der oben geschilderten Testprobleme. In den letzten Wochen hat es regelmäßig etwa 1.100.000 Tests gegeben, manchmal etwas mehr, manchmal etwas weniger. Das führt zu mehreren Schwierigkeiten. Man nimmt die Anzahl der positiv Getesteten, die unter 1.100.000 Probanden gefunden wurden und verteilt diese 56.518 Fälle so auf die Gesamtbevölkerung, als ob sie sich in schöner Regelmäßigkeit im ganzen Land in jede einzelne Gruppe von 100.000 Einwohnern einfügen würden. Wenn es insgesamt und bundesweit nur eben diese 56.518 Fälle gegeben haben sollte, dann kann man das machen. Aber immerhin wäre es auch möglich, dass eine andere Gruppe von 1.100.000 Probanden wieder eine Größenordnung von 50.000 Positiven geliefert hätte, und eine andere wieder neue Positive, was insgesamt zu einer astronomischen bundesweiten Inzidenz führen würde. Wir kennen die Dunkelziffer nicht und können sie nicht kennen, sonst wäre es keine Dunkelziffer mehr.
Ohne Frage spielt die Teststrategie eine gewisse Rolle. Sucht man beispielsweise nur symptomatische oder durch einen vorherigen Schnelltest vorbelastete Probanden aus, so wird man vermutlich höhere Werte erhalten als bei anlasslosen Massentests, sofern die Anzahl der Probanden jeweils gleich ist. Schon durch die Teststrategie kann man also den Inzidenzwert in beträchtlicher Weise steuern. Vor allem aber durch die Testanzahl, die jeder Form von Steuerung Tür und Tor öffnet. Noch einmal: Die gemeldeten 56.518 Fälle führten zu einer Inzidenz von 68 auf der Grundlage von etwa 1.100.000 Tests. Aber warum eigentlich 1.100.000 Tests? Hätte man aus der Menge der 1.100.000 Personen nur halb so viele Testungen vorgenommen, also 550.000, dann wäre es natürlich mit extrem geringer Wahrscheinlichkeit möglich gewesen, dass alle positiven Fälle in der Menge der Testpersonen zu verzeichnen wären – mit einer Inzidenz von wiederum 68 –, oder es hätten sich, mit ebenfalls äußerst geringer Wahrscheinlichkeit, alle positiven Fälle in der falschen Hälfte befunden – mit einer daraus folgenden Inzidenz von 0. Selbstverständlich ist die Wahrscheinlichkeit, dass die Zahl der Positiven in der halbierten Gruppe bei etwa der Hälfte, also ungefähr 28.000 Positiven, liegt, außerordentlich hoch. Und was passiert in diesem Fall? Schlagartig lässt sich die von der Kanzlerin so sehr gewünschte Inzidenz von 35 erreichen und unterbieten, und es macht nicht einmal Arbeit: Man muss nur die Anzahl der Tests auf die Hälfte reduzieren, und schon hat man gute Chancen, dass man nur noch den Wert 34 statt 68 erhält. Umgekehrt könnte man auch Karl Lauterbach, dem Freund der fortdauernden Apokalypse, eine Freude machen, indem man, ausreichende Laborkapazitäten vorausgesetzt, die Zahl der Tests verdoppelt und dann nach dem obigen Prinzip nicht ausschließen kann, dass aus einer Inzidenz von 68 eine Inzidenz von etwa 136 wird.
Geschmälerte Aussagekraft
Der vielbeschworene Inzidenzwert ist folglich durch Teststrategie und Testanzahl in hohem Maße steuerbar, was die schon erwähnte Schmälerung seiner Aussagekraft noch einmal steigern dürfte. Das wird noch einmal deutlich, wenn man nicht mehr bundesweite, sondern regionale und lokale Werte betrachtet. Nehmen wir beispielsweise den zur bundesweiten Betrachtung genau gegenteiligen Fall eines Dorfes von 100 Einwohnern. Einer dieser Einwohner wird getestet und erhält ein positives Resultat. Nun schlägt wieder die Berechnungsformel zu Buche, denn die Inzidenz lautet 1/100 * 100.000 = 1000. Nicht vergessen: Man teilt die Anzahl der Positiven – das ist einer – durch die Größe der relevanten Bevölkerung – das sind die 100 Dorfbewohner – und multipliziert dann mit 100.000, um als Resultat eine Inzidenz von 1000 zu erhalten. Es ist beeindruckend, wie schnell solche Werte entstehen können. Aber es kann noch schlimmer kommen, denn schließlich gibt es noch das Problem des Ct-Wertes, der von Labor zu Labor unterschiedlich sein kann. Hat ein Labor eine Grenze von 35, ab der man die weitere Replikation abbricht, und brauchte man bei unserem dörflichen Probanden gerade 35 Zyklen, so wird man ihn als positiv melden mit den geschilderten Folgen für die Inzidenz. Wird derselbe Proband von einem anderen Labor getestet, das nach 34 Zyklen abbricht, taucht er in der Statistik nicht auf. Ein kleiner Unterschied in den Laborgepflogenheiten kann bei lokaler Betrachtung einen großen Unterschied im Inzidenzwert verursachen, nämlich in diesem Fall den Unterschied zwischen 0 und 1000. Jeder kann sich ausrechnen, wie die Zahlenverhältnisse bei größeren regionalen Einheiten sein werden.
Ein weiteres Problem wurde bisher noch nicht angesprochen, und man kann es am klarsten sehen, wenn man die Frage der Umrechnung auf die Bevölkerungszahl außer Betracht lässt und sich auf eine Grundbevölkerung von 100.000 Einwohnern konzentriert: Es ist das Problem der falsch positiv Getesteten. Jeder Test, welcher Art auch immer, wird Fehler generieren, da ist ein PCR-Test keine Ausnahme. Es geht dabei nicht um irrelevant positiv Getestete, wie sie im Zusammenhang mit dem Ct-Wert und den überprüften Genabschnitten auftauchten, sondern um Probanden, die positiv getestet werden, obwohl sie eigentlich negativ sind. Solche Fehler passieren und müssen passieren, sei es durch unvermeidliche Kontaminierung, sei es durch menschliches Versagen verschiedenster Art. Der prozentuale Anteil der tatsächlich negativen Probanden, die auch wirklich als negativ erkannt werden, wird als Spezifität bezeichnet. Hat man also beispielsweise 1.000 negative Testpersonen und eine Spezifität von 99 %, so muss man damit rechnen, dass zwar 990 davon als negativ erkannt werden, 10 aber fälschlich zu den Positiven gezählt werden. In einem sogenannten Ringversuch hat man die Spezifität des PCR-Tests zu ermitteln versucht und fand einen Wert zwischen 97,8 % und 98,6 %. Da eine hundertprozentige Spezifität in der Praxis nicht möglich ist, gehen wir also für die weiteren Rechnungen davon aus, dass die Spezifität zwischen 98 % und 99,5 % liegt.

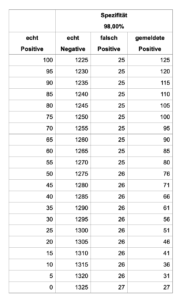
Bei einer Bevölkerung von knapp über 83 Millionen hat man innerhalb von sieben Tagen etwa 1,1 Millionen Personen getestet, das entspricht 1,325 %. Geht man nun davon aus, dass diese Testrate auch bei einer Population von 100.000 Menschen eingehalten wird, so kommt man auf 1.325 Tests, die in einer Woche durchgeführt wurden, wobei die Inzidenz auf der Basis dieser 1.325 Testergebnisse bestimmt wird. Was geschieht nun bei Inzidenzen, die sich im Bereich um 100 oder darunter bewegen? Geht man beispielsweise von 100 echt Positiven aus, so befinden sich unter den 1.325 Probanden natürlich 1.225 echt Negative. Bei einer Spezifität von 98 % – auch die anderen Werte werden später noch betrachtet – muss man aber mit einem Anteil an falsch Positiven in Höhe von 2 % rechnen, das sind in diesem Fall 2 % von 1.225, also 24,5. Zusätzlich zu den 100 tatsächlich positiven Probanden kommen also 24 oder 25 falsch positive Probanden, was zu einer gemessenen Inzidenz 124,5 führt – deutlich höher als die echte Inzidenz von 100. Es mag dabei der eine oder andere falsch Negative übersehen worden sein, aber bei einer allgemein angenommenen Sensitivität von um die 99 %, mit der man den Anteil der tatsächlich erkannten echt positiven Testfälle beschreibt, kann es sich tatsächlich nur um den einen oder anderen handeln, denn ein Prozent von 100 ist 1. Am Effekt ändert das nichts: Aus 100 echt Positiven erhält man 124,5 gemeldete Positive, was die Bedeutung dieser Kennzahl wieder einmal relativiert. Nimmt man beispielsweise nur noch 50 echt positive Fälle an, so erhöht sich die Anzahl der echt Negativen auf 1.275, und da zwei Prozent von 1.275 gerade 25,5 sind, kommen zu den 50 echten noch 25 oder 26 falsche Positive hinzu. An der Anzahl der falsch Positiven hat sich nicht viel geändert, an ihrem Anteil an den Gemeldeten allerdings sehr wohl, denn gemeldet werden jetzt 75 oder 76 Fälle, und ein Drittel davon besteht aus falsch Positiven.
Auch bei der Weltgesundheitsorganisation WHO ist man sich über diesen Effekt im Klaren. In der Information Notice vom 20.01.2021 heißt es (hier ins Deutsche übersetzt): „Die WHO erinnert IVD-Anwender daran, dass die Krankheitsprävalenz den prädiktiven Wert der Testergebnisse verändert; mit abnehmender Krankheitsprävalenz steigt das Risiko eines falsch positiven Ergebnisses. Das bedeutet, dass die Wahrscheinlichkeit, dass eine Person mit einem positiven Ergebnis (SARS-CoV-2 nachgewiesen) tatsächlich mit SARS-CoV-2 infiziert ist, mit abnehmender Prävalenz sinkt, unabhängig von der behaupteten Spezifität.“
Genau das ist der Fall, und die folgende Tabelle zeigt, wie sich bei einer Spezifität von 98 % die Beziehung zwischen echt Positiven und gemeldet Positiven entwickelt. Die berechneten Werte für falsch Positive und gemeldete Positive wurden dabei auf ganze Zahlen gerundet.
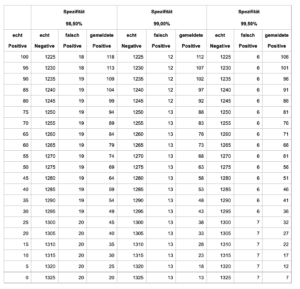
Unter den getroffenen Voraussetzungen kann man also nie unter eine Zahl von 27 gemeldeten Fällen, also unter eine Inzidenz von 27 geraten, selbst wenn kein einziger echt Positiver mehr vorhanden ist. Aber auch höhere und damit bessere Spezifitäten sollen nicht unterschlagen werden.
Nach den oben erwähnten ermittelten Spezifitäten dürfte einer der beiden Werte 98,5 % oder 99 % am plausibelsten sein, während eine Spezifität von 99,5 % nicht unbedingt realistisch ist. Dennoch kann man selbst dann bei gegebener Testzahl eine Inzidenz von 7 nicht unterschreiten, auch wenn nicht ein echt Positiver mehr zu finden ist. Im Falle der realistischeren Spezifitäten von 98,5 % oder 99 % erreicht man eine Mindestinzidenz in Höhe von 20 bzw. 13. Das Prinzip „ZeroCovid“ könnte sich somit als schwierig erweisen.
Vielleicht wird die Sache noch klarer, wenn man nicht von der Anzahl der echt Positiven ausgeht und daraus die Meldezahlen bestimmt, sondern umgekehrt die gemeldete Inzidenz zur Basis erklärt und daraus auf die Zahl der echt Positiven schließt. Dabei gehen wir von den in der zweiten Tabelle gezeigten Fällen mit einer besseren Spezifität als 98 % aus. Die nötige Formel ist leicht auszurechnen und soll hier für alle, die es nachrechnen wollen, auch angegeben werden. Wer es nicht nachrechnen will, kann die nächsten Zeilen gerne überlesen. Ist z die Anzahl der Probanden (also beispielsweise 1.325), s die Spezifität (also beispielsweise 0,99) und ep die Anzahl der echt Positiven (also beispielsweise 100), so berechnet man die Zahl der echt Positiven aus der Inzidenz nach der Formel ep = (Inzidenz – z + s*z) / s. Für 1.325 Probanden, eine Spezifität von 99 %, also 0,99, und eine gemeldete Inzidenz von 100 ergibt sich auf diese Weise eine Anzahl von (100 – 1.325 + 0,99 * 1325) / 0,99=87,6. Von 100 gemeldeten Positiven sind daher unter den gegebenen Bedingungen nur 87 oder 88 echt positiv. Die folgende Tabelle zeigt die damit berechneten Werte bei verschiedenen gemeldeten Inzidenzen und verschiedenen Spezifitäten, mit wiederum ganzzahlig gerundeten berechneten Werten.
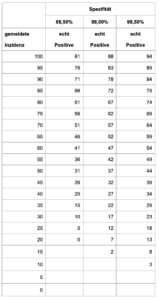
Über die leeren Felder muss man sich nicht wundern, sie sind unvermeidlich. Hat man beispielsweise eine Spezifität von 98,5 % und eine Inzidenz von 20, so ist gerade noch Platz für keinen einzigen echt Positiven. Eine Inzidenz von 15 oder tiefer ist bei dieser Spezifität und dieser Testzahl gar nicht mehr mit einer korrekten Anzahl echt Positiver zu erreichen, da die Quote der Falsch-Positiven alles in Beschlag nimmt.
Ist man nun freundlich und geht von 99 % Spezifität aus, so findet man bei der Inzidenz 50 noch 37 echt Positive, bei 40 sind es nur noch 27 und bei 15 verbleiben gerade noch 2. Vergleichsweise niedrige gemeldete Inzidenzen können zu großen Teilen auf falsch positiven Testungen beruhen. Und auch diese Betrachtung zeigt: Das Ziel „ZeroCovid“ dürfte mangels Erreichbarkeit zu Problemen führen.
Abhängigkeit von den Testzahlen
Aber, so könnte man fragen, hatte man nicht im Sommer sehr niedrige Inzidenzen zu verzeichnen? Das hatte man, und es zeigt ein weiteres Mal den Grad der Beliebigkeit, der an der Inzidenz haftet. In den Sommerwochen wurden deutlich weniger Testungen vorgenommen als zur Zeit, in einer Größenordnung von etwa 400.000 pro Woche. Das sind 0,48 % der Gesamtbevölkerung, und entsprechend sollte man davon ausgehen, dass in unserer fiktiven Population von 100.000 Menschen ebenfalls 0,48 % einem Test unterworfen wurden, das sind dann 480. Statt 1.325 Probanden stehen somit nur noch etwa 480 zur Verfügung. Führt man mit diesem Wert die oben beschriebenen Rechnungen durch, so findet man, dass je nach Spezifität eine gemeldete Inzidenz unter 5 erreichbar ist – nicht weil sich die Verhältnisse geändert hätten, sondern weil weniger getestet wurde. Es ist das gleiche Phänomen, das bereits oben beschrieben wurde.
Noch immer sind nicht alle Aspekte untersucht, denn es stellt sich nun die Frage, ob die zukünftig in großer Zahl vorgesehenen Schnelltests einen weiteren Einfluss auf die Inzidenz haben werden. Um den Umfang dieses Beitrags nicht über Gebühr anwachsen zu lassen, muss diese Frage aber einem späteren Artikel vorbehalten bleiben.
Man hört das Wort „Inzidenz“ und meint, „es müsste sich dabei doch auch was denken lassen,“ um noch einmal Mephistopheles zu bemühen. Das ist auch der Fall, es lässt sich vieles denken. Die Inzidenz ist abhängig vom Ct-Wert und der Suchstrategie des PCR-Tests. Sie wird beeinflusst von der Teststrategie und ganz besonders von der Testanzahl. Sie kann in Bezug auf kleinere Bevölkerungseinheiten aus kleinen Ursachen große Wirkungen erzeugen. Und man muss zu ihrer Beurteilung die Rate falsch positiver Testungen berücksichtigen. Sehr viele Nebenbedingungen für eine einzige Zahl. Wie es scheint, ist das Wort „Inzidenz“ ein gutes Beispiel für eine andere Anmerkung des teuflischen Mephistopheles:
„Mit Worten lässt sich trefflich streiten,
Mit Worten ein System bereiten,
An Worte lässt sich trefflich glauben,
Von einem Wort lässt sich kein Jota rauben.“

Gastbeiträge geben immer die Meinung des Autors wieder, nicht meine. Ich schätze meine Leser als erwachsene Menschen und will ihnen unterschiedliche Blickwinkel bieten, damit sie sich selbst eine Meinung bilden können.
Thomas Rießinger ist promovierter Mathematiker und war Professor für Mathematik und Informatik an der Fachhochschule Frankfurt am Main. Neben einigen Fachbüchern über Mathematik hat er auch Aufsätze zur Philosophie und Geschichte sowie ein Buch zur Unterhaltungsmathematik publiziert.
Michael Horn ist Mathematiker und wechselte nach seinem Studium in die Zentrale Forschung eines großen Dax-Unternehmens. Nach weiteren Stationen in der Strategischen Planung, Marketing, Leitung Produktmanagement für eine Hochverfügbarkeits-IT-Plattform, ist er inzwischen in ein anderes Dax-Unternehmen gewechselt und dort für das Global Reporting im Weiterbildungsbereich verantwortlich.
Bild:FrankHH/Shutterstock
Text: Gast
mehr von Prof. Thomas Rießinger auf reitschuster.de

[themoneytizer id=“57085-1″]